신호 및 시스템 7 - 컨볼루션(Convolution)

1. 컨볼루션 적분의 정의
$$ y(t)= \int_{- \infty }^{ \infty } x ( \tau )h(t- \tau )d \tau =x(t) \ast h(t) $$
위 수식에서 임펄스 응답인 h(t)를 알고 있으므로
임의 입력에 대한 선형 시불변(LTI) 시스템 응답인 y(t)을 구할 수 있습니다.
2. 컨볼루션 연산
미끄럼 방식 계산법
한 신호를 뒤집어 시간축의 좌측부터 끌고오며 곱한 결과를 모드 더하는 연산
2-1. 컨볼루션 예시

위에서 y(t)=x(t)*h(t)일때 y(t)를 구해보겠습니다.
1. 두시간의 시간축을 t에서 τ로 변환합니다.
$$ x(t) \longrightarrow x( \tau ),h(t) \longrightarrow h( \tau ) $$
2. 신호 하나를 고정하고 다른하나를 시간 반전 합니다.
$$ x( \tau )그대로, h( \tau ) \longrightarrow h( -\tau ) $$
3. 시간 반전된 신호를 τ 축에서 시간이동 시킨 h(t−τ)가 x(τ)에 겹쳐지는 것을 구간별로 나눕니다.
[ (1) t<0 안겹침 ]

[ (2) 0≤t<1 부분겹침 (시간이 지날수록 겹침 증가) ]

[ (3) t=1 전체겹침 ]

[ (4) 1<t≤2 부분겹침 (시간이 지날수록 겹침 감소) ]
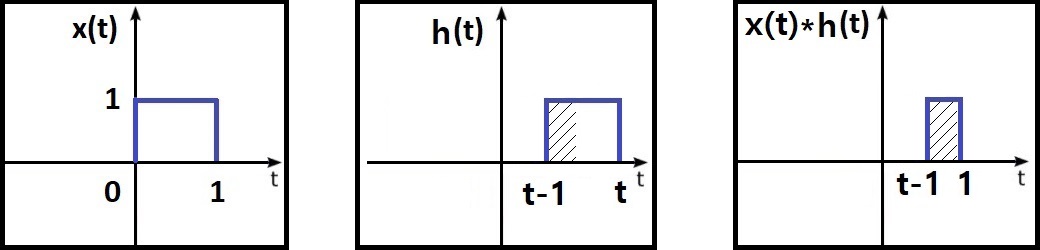
[ (5) t>2 안겹침 ]

4. 겹치는 구간에 대해서 적분 계산을 합니다.
$$ 0 \leq t < 1 : y(t)= \int_0^t 1d \tau =t $$
$$ t =1 : y(t)= \int_0^1 1d \tau =1 $$
$$ 1<t \leq 2:y(t)= \int_{t-1}^{1}1d \tau =-t+2 $$
5. 위 과정으로 만들어진 면적의 양과 식을 보고 결과를 얻을 수 있습니다.

3. 컨볼루션의 성질
[ 교환법칙 ]
$$ x(t) \ast h(t)=h(t) \ast x(t) $$
[ 결합법칙 ]
$$ (x(t) \ast h_{1}(t)) \ast h_{2}(t)=x(t) \ast (h_{1}(t) \ast h_{2}(t)) $$
[ 배분법칙 ]
$$ x(t) \ast (h_{1}(t) + h_{2}(t))=x(t) \ast h_{1}(t) + x(t) \ast h_{2}(t) $$
[ 이동 성질 ]
$$ y(t-t_{0})=x(t-t_{0}) \ast h(t) $$
[ 임펄스와 컨볼루션 ]
$$ x(t) \ast \delta (t-t_{0})=x(t-t_{0}) $$
[ 길이와 끝 ]
$$ x(t)=0, t<t_{1},t>t_{2} $$
$$ h(t)=0, t<t_{3},t>t_{4} $$
일때
$$ y(t)=x(t) \ast h(t), t<t_{1}+t_{3},t>t_{2}+t_{4} $$