
1. 단위 계단 함수 (Unit step function)
$$ u(t)=\begin{cases}1 & t > 0\\0 & t < 0\end{cases} $$

ex)
단위 계단 함수를 사용하면 원하는 부분의 신호 값을 사용할 수 있습니다.

2. 사각 펄스 함수(Rectangular pulse function)
$$ rect( \frac{t}{2a} ) =\begin{cases}1 & -a < t < a\\0 & else\end{cases} $$
$$ rect( \frac{t}{2a} ) =u(t+a)-u(t-a) $$

3. 부호 함수 (Signum function)
$$ sgn(t) =\begin{cases}-1 & t < 0\\0 & t=0\\ +1&t > 0\end{cases} $$

4. 램프 함수 (Ramp function)
$$ r(t)=\begin{cases}t & t \geq 0\\0 & t < 0\end{cases} $$

※ 램프 함수와 계단 함수의 관계 ※
$$ \int_{- \infty }^t u( \tau )d \tau =tu(t)=r(t) $$
※ 계단 신호와 램프 신호 ※
계단 신호 : 급작스러운 입력 값 변화에 대한 시스템 반응
램프 신호 : 시간에 비례하여 증가하는 입력에 대한 시스템 반응
5. 삼각 펄스 함수 (Triangular pulse function)
$$ tri(t)=\begin{cases}1- | t | & | t | \leq 1\\0 & | t | > 1\end{cases} $$

6. 단위 임펄스 함수 (Unit impulse function)
$$ \delta (t) =\begin{cases} \infty & t = 0\\0 & t \neq 0\end{cases} $$
$$ \int_{- \infty }^ \infty \delta (t)dt =1 $$
$$ \delta (t)=\delta (-t) $$

※ 임펄스 함수의 샘플링 성질 ※
임펄스 함수는 t=0 일 때 만 값이 존재하므로 원하는 값을 사용하기 용이합니다.
$$ x(t)\delta (t-t_{0})=x(t_0)\delta (t-t_{0}) $$
$$ \int_{- \infty }^ \infty x(t)\delta (t-t_{0})dt =x(t_{0}) \int_{- \infty }^ \infty \delta (t')dt '=x(t_0) $$
※ 임펄스 함수와 계단 함수의 관계 ※
$$ \delta (t)= \frac{du(t)}{dt} $$
$$ u(t)= \int_{- \infty }^{t} \delta ( \tau )d \tau $$
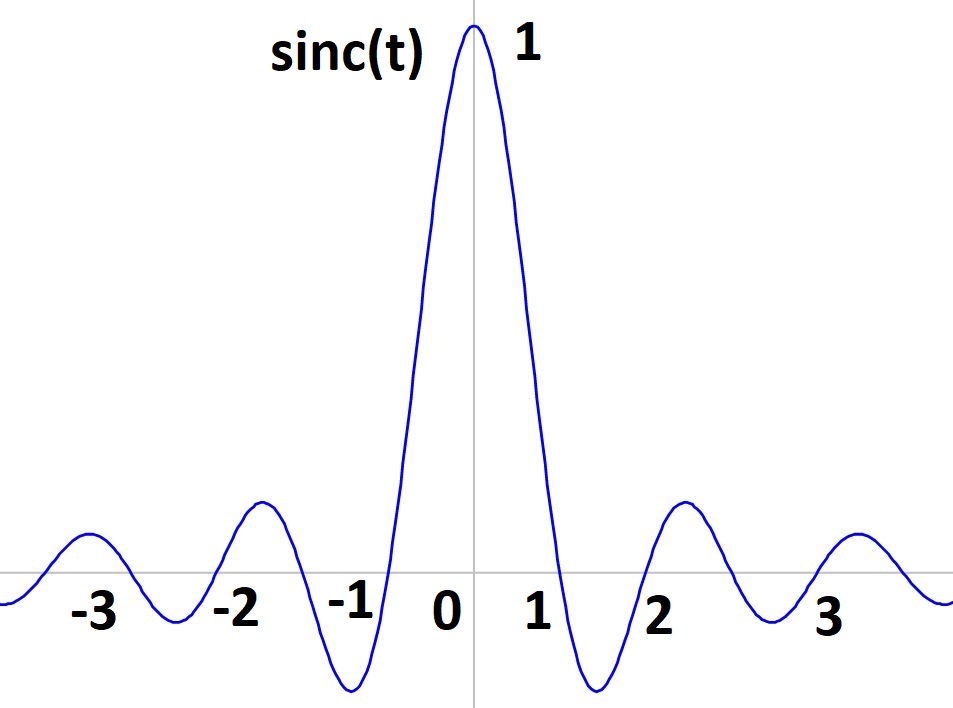
7. 싱크 함수 (Sinc function)
$$ sinc(t)= \frac{sin \pi t}{ \pi t} $$
'전자 > 신호 및 시스템' 카테고리의 다른 글
| 신호 및 시스템 6 - 임펄스 응답 (0) | 2022.01.22 |
|---|---|
| 신호 및 시스템 5 - 시스템 응답의 구분 (0) | 2022.01.21 |
| 신호 및 시스템 4 - 연속 신호 연산 (0) | 2022.01.20 |
| 신호 및 시스템 2 - 신호의 분류 (0) | 2022.01.18 |
| 신호 및 시스템 1 - 신호 및 시스템 기초 (0) | 2022.01.17 |



