확률 및 랜덤프로세스 2 - 신호 및 시스템 기본 1

- 다음 글 -

신호 및 시스템 기본 2

https://p-rove.tistory.com/32

---

1. 연속신호와 이산신호

 연속신호와 이산신호

연속 신호 : 끊기지 않는 연속적인 시간으로 표현

 

이산 신호 : 연속적이지 않은 점들의 집합으로 표현

---

2. 실 신호와 복소 신호

실 신호 : 신호의 값이 실수인 신호

 

복소 신호 : 신호의 값이 복소수인 신호

---

3. 주기 신호와 비주기 신호

주기 신호 : 일정한 신호 모양이 주기적으로 반복되는 신호

 

비주기 신호 : 주기적으로 반복되지 않는 신호

(주기가 무한대인 주기 신호로도 볼 수 있습니다.)

---

4. 에너지 신호와 전력 신호

에너지 신호 : 신호의 에너지가 유한한 값을 가지는 신호

$$ E =  \lim_{T \rightarrow  \infty }  \int_{-T}^{T}  |  x^{2}(t)  |  dt  $$

 

전력 신호 : 신호의 평균전력이 유한한 값을 가지는 신호

$$ P =  \lim_{T \rightarrow  \infty }  \frac{1}{T}  \int_{-T/2}^{T/2}  |  x^{2}(t)  |  dt  $$

---

5. 단위 임펄스 함수

정의

$$  \int_{ \alpha }^{ \beta } f(t) \delta (t- t_{0} )dt =  \begin{cases}f_{0} &  \alpha  \leq  t_{0}  \leq  \beta \\0 & else\end{cases}  $$

 

면적 특성

$$ \int_{ -\infty }^{ \infty }  \delta (t)dt = 1  $$

 

표본화 특성

$$ \int_{ -\infty }^{ \infty }  x(t)\delta (t)dt = x(0) \int_{ -\infty }^{ \infty } \delta (t)dt = x(0) $$

---

6. 단위 계단 함수

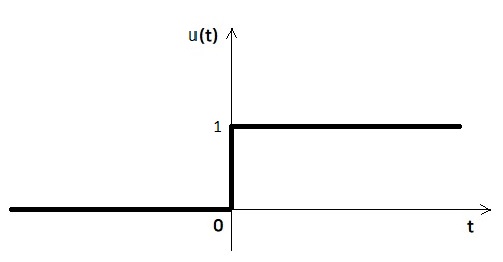
정의

$$ u(t) =\begin{cases}1 & t  \geq  0\\0 & t  <  0\end{cases}  $$

 

추가

$$ u(t) = \int_{- \infty} ^{t}  \delta ( \tau ) d \tau  =\begin{cases}0 & t  <  0\\1 & t   \geq   0\end{cases}  $$

 

$$ \frac{du(t)}{dt} =  \delta (t)  $$

 

---

7. Sinc 함수

정의

$$ sinc(x)  =\begin{cases}sin( \pi x)/( \pi x) & x \neq 0\\1 & x = 0\end{cases}  $$

---

- 다음 글 -

신호 및 시스템 기본 2

https://p-rove.tistory.com/32